
aus spektrum.de, 12. 9. 2021 zu Jochen Ebmeiers Realien
Wenn Zahlen unberechenbar werden
Wenn der Taschenrechner kapitulieren muss, gibt es nur noch eine Rettung: die Näherung!
von Florian Freistetter
Früher
habe ich gerne mit den Buchstaben meines Namens gespielt. Wie
vermutlich alle Kinder habe ich ausprobiert, wie er sich rückwärts
liest. »Nairolf« lässt sich zwar immerhin aussprechen, richtig
begeistert war ich davon nicht. Aber egal, wie ich die Buchstaben
umgestellt habe, es ist nichts Brauchbares dabei herausgekommen. Ich
habe probiert, alle Möglichkeiten zu testen.
Hätte ich jedoch damals schon berechnen können, wie viele das sind, hätte ich
es vermut-lich gar nicht erst versucht. Die sieben Buchstaben meines
Vornamens kann ich auf 5040 unterschiedliche Weisen schreiben. Würde ich
auch noch meinen Nachnamen dazunehmen, wären es deutlich mehr (über
eine Billion Varianten). Zentral für diese Rechnung ist die Operation
der Fakultät, die mathematisch mit einem ! ausgedrückt wird
(n! = 1 · 2 · 3 ·...· n).
Mein Taschenrechner schafft gerade noch die Berechnung von 69! – der Versuch, auch 70! auszurechnen, liefert eine Fehlermeldung. Das Ergebnis wäre eine Zahl mit mehr als 100 Stellen, und dafür reicht der Speicher nicht. Um dennoch zumindest ein näherungswei-ses Ergebnis zu erhalten, kann man sich dieser Formel bedienen:
Zu den einzelnen Elementen dieser Formel siehe Fakultät (!), Quadratwurzel (√), Kreiszahl (π) und Eulersche Zahl (e).
Auch daran scheitert mein Taschenrechner – aber zumindest hat man es nun mit Rechenoperationen zu tun, die ein wenig einfacher zu handhaben sind als die Fakultät. Das hilft zum Beispiel dann, wenn man nicht an einer exakten Zahl als Ergebnis interessiert ist, sondern lediglich wissen will, wie viele Stellen die Zahl hat. Die folgt ja aus dem Logarithmus zur Basis 10 der entsprechenden Zahl, und so eine Rechnung kann man mit der rechten Seite der Formel wesentlich leichter ausführen als mit der linken.
Die nach dem schottischen Mathematiker James Stirling benannte Formel ist aber nicht nur wichtig, wenn man die Anzahl der Vertauschung von Buchstaben eines langen Namens berechnen möchte. Auch in der Wissenschaft ist es unter Umständen nötig, solche großen Zahlen zu bestimmen. Zum Beispiel beim »Einstein-Modell : Schon 1907 hat Albert Einstein eine quantenmechanische Beschreibung für die Wärmekapazität von Festkörpern entwickelt.
Darin modellierte er den Körper als
System von harmonisch schwingenden Atomen, deren Schwingungsenergie nur
quantisierte Werte annehmen kann. Will man damit zum Beispiel Größen wie
die Entropie des Körpers bestimmen, taucht in der entsprechenden Formel
eine Zahl auf, die sich aus der Fakultät der Anzahl der schwingenden
Atome berechnet. Davon hat so ein Festkörper aber jede Menge, und die
Gleichung ist nur durch die Näherung von Stirling einigermaßen in den
Griff zu kriegen. Das könnte Sie auch interessieren: Spektrum der Wissenschaft Spezial Physik – Mathematik – Technik 3/2021
Das könnte Sie auch interessieren: Spektrum der Wissenschaft Spezial Physik – Mathematik – Technik 3/2021
Algorithmen für die Zukunft
In der Thermodynamik hat man es auch abseits von Einsteins
Modell immer wieder mit Fakultäten großer Zahlen zu tun. Sie tauchen
meist bei der Berechnung der Entropie oder ähnlicher Eigenschaften auf.
Und bei der Avogadro-Konstante: Sie gibt an, wie viele Teilchen – Atome
oder Moleküle – in einer Stoffmenge von einem Mol enthalten sind. Per
Definition sind es exakt 6,02214076 · 1023, und wenn man
diese Zahl in Verbindung mit einer Fakultät vor sich hat, lernt man den
Wert der Stirling-Näherung sehr zu schätzen.
Bei meiner Beschäftigung mit den Anagrammen meines Namens bin ich solch großen Zahlen nie auch nur nahe gekommen. Heute muss man die Kombinationen nicht mehr selbst durchprobieren, so wie ich es als Kind getan habe. Entsprechende Computerpro-gramme können das mittlerweile viel schneller, und eines davon hat mich gerade informiert, dass man meinen vollständigen Namen zu »Affe einsortiert RTL« umordnen kann. Hätte ich das nur schon als Kind gewusst!
Nota. - Ab einem bestimmten Punkt - eigentlich einem unbestimmten Fleck - ist das Rechnen mit Zahlen (uns) faktisch unmöglich, und wenn der Computer einspringt, kann man doch nichts damit anfangen. Die Zahl Pi ist inzwischen angeblich bis auf 62 (oder 620?) Billionen Stellen hinterm Komma ausgerechnet worden. Ist dafür eine praktische Anwendung denkbar?
Rein gedanklich hat es seinen Wert, nämlich mindestens die Einsicht, dass auch dann noch ein Rest übrig ist. Wenn Pi von irgendeiner Intelligenz der Konstruktion des Kreises zu Grunde gelegt worden wäre, müsste sich irgenwann eine endliche Zahl auffinden lassen.
Doch kein gesunder Geist würde einen Kreis aus Zahlen aufbauen wollen. Man wählt anschaulich einen Punkt im Raum und bewegt eine gerade Linie rundherum. Doch das ergibt immer nur diesen einen Punkt, diese eine Linie und diesen einen Kreis. Der Kreis "als solcher" lässt sich nur - durch Zahlen darstellen. Hätte eine Intelligenz den Kreis erschaffen wollen, hätte sie alle möglichen Kreise anfertigen müssen. Anfertigen? Fertig wäre sie bis heute nicht, so groß wäre ihre Zahl; nämlich ∞. Denn dies ist die Pointe: Dem Unendlichen kann man sich nicht annähern. So weit man es auch treibt, der Abstand bleibt immer derselbe: unendlich. Allerdings gibt es eine Richtung vor.
JE.
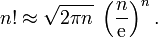
Keine Kommentare:
Kommentar veröffentlichen